by A. Andales1 (12/14)
Quick Facts….
- Variability in evapotranspiration demand and precipitation causes irrigation requirements to change from year to year.
- Past records of seasonal evapotranspiration and precipitation can be used to plan ahead for irrigation requirements that will probably occur.
- The amount and timing of precipitation (P) and evapotranspiration (ET) demand are the two main weather-related variables that determine irrigation requirements.
- A crop will attain its yield potential as long as its ET demand is satisfied throughout the growing season and all other growth factors are non-limiting.
The irrigation requirements of a crop are affected by weather variability. The amount and timing of precipitation (P) and evapotranspiration (ET) demand are the two main weather-related variables that determine irrigation requirements. The ET demand of a crop is a measure of how much water can be consumed via soil evaporation and plant transpiration assuming that plant-available water is adequate. The ET demand varies from day-to-day depending on crop growth stage and weather variables such as solar radiation, air temperature, humidity, and wind conditions. The daily ET demand of a crop can be estimated from daily measurements of the weather variables previously mentioned.
Assuming that all other growth factors are non-limiting – meaning conditions are such that these factors remain favorable to crop growth – a crop will attain its yield potential as long as its ET demand is satisfied throughout the growing season. Yield reductions occur when the ET demand is not satisfied, especially during critical growth stages (for example, reproductive and grain filling stages). The ET demand can be satisfied by precipitation, stored soil moisture in the root zone, and/or irrigation. Irrigation becomes necessary when natural precipitation and stored soil moisture are not adequate to satisfy all of the ET demand.
An example of the seasonal variability of ET demand and precipitation is shown in Figure 1 for the Colorado State University (CSU) – Agricultural Research, Development and Education Center (ARDEC) located northeast of Fort Collins, Colorado. The corn ET demand and precipitation from May to August of each year was obtained from the Colorado Agricultural Meteorological Network (CoAgMet) crop ET access page (http://ccc.atmos.colostate.edu/cgi-bin/extended_etr_form.pl) for the available period of record (1992-2008). Instructions for using this online tool are available on the website above. For this example, corn ET demand was calculated assuming a May 1 planting date each year.
There were 17 years between 1992 and 2008. However, 24 days of data were missing from the 2003 seasonal record at ARDEC and no nearby weather station could be used in its place. Therefore, 2003 was excluded from the analysis. Also, 28 days of data were missing from the 2008 seasonal record because of tornado damage of the weather station. A complete record for 2008 from a nearby weather station (Wellington) was used instead. For the 16 years of usable record available from CSU-ARDEC, the average seasonal (May to August) corn ET demand was 20.2 inches while average precipitation for the same period was only 6.5 inches (only 32 percent of corn ET demand).
This meant that the average shortfall (ET − P) was 13.7 inches, which would have had to be satisfied by stored soil moisture and/or irrigation. The quantity ET − P (that is, ET minus P) can also be used as a rough estimate of irrigation requirement. Actual stored soil moisture at planting must be subtracted from this quantity to get a better estimate of the seasonal irrigation requirement. It is also important to note that not all precipitation amounts are effectively available to the crop because of runoff and deep percolation losses from the root zone. Figure 1 shows that ET demand, precipitation, and irrigation requirements can vary greatly from year-to-year. This figure shows how the weather in each year (represented by ET and P) affects irrigation requirement (represented by ET − P). The water shortfall was highest in 2006 (ET − P = 21.2 inches) and lowest in 1995 (ET − P = 3.5 inches).
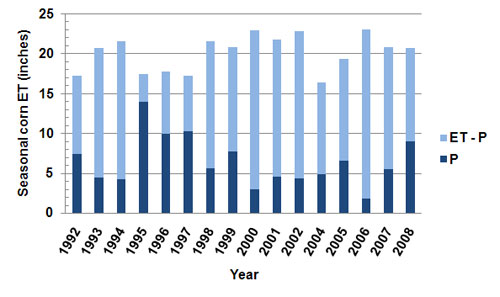 |
| Figure 1. Total corn evapotranspiration (ET) demand per season (May to August) at CSU-ARDEC near Fort Collins from 1992 to 2008. The year 2003 was not included because of missing data. Part of the ET demand can be satisfied by precipitation (P) while the remainder (ET − P) must be satisfied by stored soil moisture or irrigation. |
Probable Irrigation Requirements
It is difficult to say with certainty what a crop’s irrigation requirement will be for the coming season. This is because weather, specifically precipitation and ET demand, are difficult to predict. However, past records of P and ET can be used to estimate the probability (chance of occurrence) that certain amounts of P, ET, and corresponding shortfalls (P − ET) will occur at a location. Then, depending on the level of risk we are willing to take; we can select a level of probability (50 percent for example) and determine the corresponding crop ET demand that will likely occur. We can then plan ahead to ensure that we have enough water to supply the ET demand that will likely occur. Simple frequency analysis of P and ET can be performed to estimate the chances based on past weather records.
A time series of values (for example, a record of seasonal ET demand over many years) can be plotted graphically against the probabilities that these values will be exceeded. The “probability of exceedance” (Pe) can be expressed as the percentage of time that the value being considered will be exceeded. The Weibull formula is a standard method of estimating a value’s probability of exceedance and is commonly used in hydrology. It is given by the equation below [Source: Chow, V.T., Maidment, D.R., Mays, L.R. (1988) Applied Hydrology, McGraw-Hill, Inc., New York, p.396]:
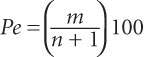
where m is the rank of a value in a list arranged from highest to lowest and n is the total number of observations or values. For instance, the highest value will have a rank of 1 while the lowest value will have a rank of n. As with any statistical procedure, having more data (large n) is better than having few data (small n).
| Table 1. Ranked values of seasonal (May to August) corn ET demand at CSU-ARDEC and their assigned probability values. | |||
| Year | Corn ET (in) | Rank, m | Probability of exceedance, % |
| 2006 | 23.07 | 1 | 5.9 |
| 2000 | 23.01 | 2 | 11.8 |
| 2002 | 22.88 | 3 | 17.6 |
| 2001 | 21.80 | 4 | 23.5 |
| 1994 | 21.60 | 5 | 29.4 |
| 1998 | 21.58 | 6 | 35.3 |
| 2007 | 20.92 | 7 | 41.2 |
| 1999 | 20.91 | 8 | 47.1 |
| 1993 | 20.77 | 9 | 52.9 |
| 2008 | 20.75 | 10 | 58.8 |
| 2005 | 19.37 | 11 | 64.7 |
| 1996 | 17.84 | 12 | 70.6 |
| 1995 | 17.49 | 13 | 76.5 |
| 1997 | 17.27 | 14 | 82.4 |
| 1992 | 17.22 | 15 | 88.2 |
| 2004 | 16.39 | 16 | 94.1 |
As an example, the data from CSU-ARDEC (Figure 1) was plotted versus their probabilities of exceedance. Table 1 shows the ranking of seasonal corn ET demand from highest to lowest. The probabilities in the right-most column were calculated using the Weibull formula. The same procedure was applied (data not shown) to seasonal precipitation and water shortfall (ET − P).
Figure 2 shows that the relationship between corn ET demand and exceedance probability can be approximated by a straight line (linear trend line fitted through the points by a graphing program like Microsoft Excel®). The straight line accounts for about 94 percent of the variability of corn ET demand depending on exceedance probability (r2 = 0.94). From the graph, one can see that 50 percent of the time, seasonal corn ET demand was equal to or greater than 20 inches of water. Seasonal corn ET demand was at least 17 inches 80 percent of the time while it was at least 22.5 inches 20 percent of the time. From the graph, one can get an estimate of how often a certain value of corn ET demand at CSU-ARDEC was equaled or exceeded.
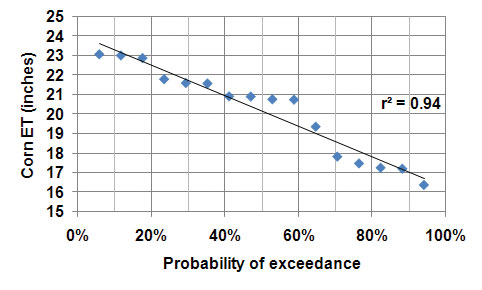 |
| Figure 2. Probabilities (chances) of exceeding different values of seasonal corn ET (May to August) at CSU-ARDEC for the period 1992-2008. |
For example, if we want to be 80 percent sure that our water supply (stored soil moisture + irrigation water) will be enough to satisfy corn ET demand, then we should determine the seasonal corn ET that is exceeded only 20 percent of the time (Pe = 100 − 80 = 20%). Corn ET with 20 percent exceedance probability means that it will not be exceeded 80 percent of the time. From Figure 2 at 20 percent probability of exceedance, the expected seasonal corn ET is 22.5 inches. Therefore, we should make plans to have a total of 22.5 inches of water available for the season (stored soil moisture and/or irrigation water). In this example, we are taking a 20 percent chance (risk) that our water supply will not be enough to satisfy corn ET demand. Producers who are willing to take more risks can select a higher probability of exceedance.
Likewise, seasonal precipitation (May to August) was plotted against probability (Figure 3). In this case, precipitation versus probability was not linear, so the horizontal axis was converted to a logarithmic scale (base 10 logarithmic scale in Microsoft Excel®). This means that the probability changes rapidly as seasonal precipitation varies. In hydrology, a logarithmic scale is often used to make the probability graph appear linear. Sometimes, we are interested in unknown values between two adjacent observations. Interpolation is the process of estimating unknown values between actual observations based on observed trends. Converting data to their logarithmic values makes interpolation easier, since a straight trend line is much simpler than a curved trend line. From Figure 3, it can be estimated that seasonal (May to August) precipitation at CSU-ARDEC was at least 5.5 inches 50 percent of the time. The plot shows that seasonal precipitation was at least 4 inches 80 percent of the time while it was at least 9 inches 20 percent of the time.
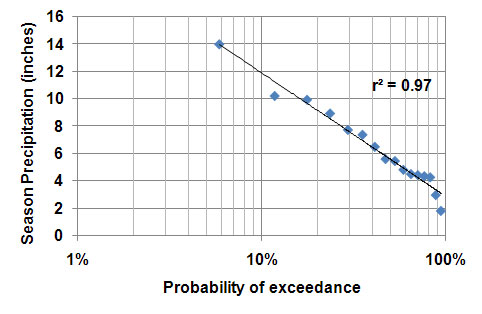 |
| Figure 3. Probabilities (chances) of exceeding different values of seasonal precipitation (May to August) at CSU-ARDEC for the period 1992-2008. |
As mentioned earlier, the water shortfall represented by (ET − P) can be a rough estimate of irrigation requirements. The probability graph of this requirement for corn at CSU-ARDEC is linear (Figure 4). Half of the time (50 percent probability), the water shortfall was at least 13 inches. The water shortfall was at least 8.5 inches, 80 percent of the time, while it was at least 18 inches 20 percent of the time.
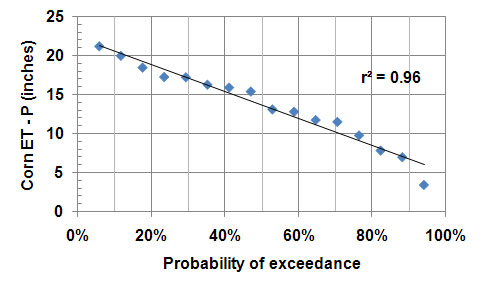 |
| Figure 4. Probabilities (chances) of exceeding different values of seasonal (May to August) water shortfalls (ET − P) at CSU-ARDEC for the period 1992-2008. |
Caution Needed in Interpreting Probabilities
Probability graphs, like the ones given above, are only as reliable as the individual data points used to make them. At times, there may be outliers – data points that are extremely high or low because of errors in data collection (a malfunctioning rain gauge, for example). Outliers may need to be excluded from the data series to get a more reliable probability plot. Also, having more data points in time gives more credibility to the probability graph. In the above example, the year 2003 was excluded because it had 24 days of missing records, which would have caused an under-estimation of ET and P for that year. As more years are added to the historical record of ET and P at CSU-ARDEC (and all other CoAgMet stations), these can be included in updated versions of the probability graphs.
There is a danger in estimating probabilities outside of the available data range (extrapolation). For example, estimating the probability of 16 inches of seasonal precipitation from Figure 3 would not be a good idea. Probability plots are most reliable in the middle of the data range, where more data have been recorded or observed. That is why longer periods of record are better, because more extreme (very high or very low) values would have been recorded.
Statisticians use statistical tests of the data to improve the reliability of probability plots and to fit appropriate lines through the data points. Only a simplistic approach is given here to illustrate how weather variability can affect irrigation water requirements.
1A. Andales, Colorado State University Extension irrigation specialist and Associate Professor, soil and crop sciences. 12/14.
Colorado State University, U.S. Department of Agriculture, and Colorado counties cooperating. CSU Extension programs are available to all without discrimination. No endorsement of products mentioned is intended nor is criticism implied of products not mentioned.
Go to top of this page.





